3S（スリーエス）とは、 稲盛研究助成 を受けた研究者から構成される「盛和スカラーズソサエティ（Seiwa Scholars Society）」の略称です。3Sでのつながりをきっかけにその多様な専門性の交流が深まることで、助成対象者の研究がさらに発展していくことを願い、1997年から活動してきました。連載「3S研究者探訪」では、さまざまな分野で活躍する3Sの研究者へのインタビューをお届けしています。第12回は、名古屋大学の谷本祥（たにもと・しょう）氏＝2019年助成対象者＝の研究室を訪問してきました。

複数の項と変数を持つ方程式によって定まる図形の上に、有理点がいくつあるか──。そんなことを考える分野の有名な問題に、「Manin（マニン）予想」というものがあります。名古屋大学の谷本祥氏は、このManin予想の研究者として、この分野で大きな成果を上げてきました。しかし、「Manin予想の研究」と聞いても、数学者以外の人にとってはおそらく、何のことか全く分からないでしょう。いったいManin予想とは何なのか、この問題について研究することにはどんな意味があるのか、数学を研究するとはどういうことか。谷本氏に尋ねました。

──谷本先生が研究されている「Manin予想」とは、どのようなものでしょうか。普段数学と距離のある人にもわかりそうな感じで、教えていただけたら…。

谷本祥氏（以下敬称略）　はい、やってみます（笑）。まず大きな枠組みから説明すると、数学の一分野に、ディオファントス幾何学というものがあります。詳しくは追ってお話ししますが、ひとまず、Manin予想とは、ディオファントス幾何学における一つの予想、だと言えます。1980年代後半にユーリ・マニン（Yuri Manin）とその共同研究者によって提唱されました。

では、ディオファントス幾何学とは何か。

まず、円や円すいといった図形を思い浮かべてみてください。円が\(x^2+y^2=r^2\)と書けるように、これらの図形は、\(x, y, z\)などの変数を使った方程式で表すことができます。

\(x^3+y^3+z^3+w^3=0\) を表す3次曲面の模型

このように、多変数多項式の方程式で定まる幾何的図形のことを代数多様体と言います。たとえば、\(x^3+y^3+z^3+w^3=0\)という方程式は、上の図のような3次元空間の曲面として描くことができます。さらに複雑で高次元の方程式についても、絵で描いたり模型を作ったりすることはできなくても、各々その次元における幾何的性質を持った代数多様体に対応します。

ディオファントス幾何学とは、このような代数多様体の上にある有理点、つまり座標が有理数で与えられる点について研究する学問です。ではManin予想とは何か。ざっくり言えば、代数多様体のうち「Fano（ファノ）多様体（※1）」と呼ばれるタイプの多様体上にある有理点について、その個数には一定の法則がある、という予想です。つまり、あらゆるFano多様体上の有理点の個数は、その多様体の幾何学的特性を反映した一つの式によって表現できるというのがManin予想の主張なのです。

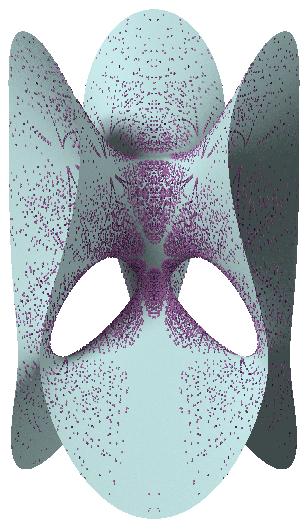
クレブシュ3次曲面上の27本の線の外側にある高さのある有理点　ⒸDrs. Ulrich Derenthal and Oliver Labs

予想について考えることが新しい数学を生み出す

──なるほど、つまりManin予想とは、代数多様体という幾何的図形の上にある有理点の個数についての予想なのですね。しかしそもそも、このような予想について研究するのはなぜなのでしょうか。幾何的図形上にある有理点について考えたり、その個数を数えたりすることには数学上どういう意味があるのか、知りたいです。

谷本　Manin予想について研究する意味を問われると、答えるのは簡単ではありません。実際、有理点の個数を数えたりすることに数学上何か意味があるのかといえばそうでもないし、Manin予想が証明できたら、何かすぐに役に立つというわけでもないからです。しかし、ではこのような研究することに意味がないのかといえば決してそうではありません。

たとえば、ディオファントス幾何学における有名な問題として、「フェルマーの最終定理」があります。これは、17世紀の数学者フェルマーが、「自分はその証明を見つけたがここにはそれを書くスペースがない」という言葉とともに書物の余白に書き残した定理で、証明されるまでに350年もの時間がかかったことで広く知られています。

この問題も曲線上の有理点の数に関するもので、証明すること自体に何か数学的な意味や応用性があったかといえば、特にありません。しかし一方、これを証明しようと350年もの間、多くの人が悪戦苦闘していた中で、たくさんの新しい数学が生まれました。つまり、数学の世界をより豊かなものにするのに大きく貢献したのです。

Manin予想も同様です。やはり、証明できたら何かに応用できる、というものではありません。しかし証明するためには、代数・幾何・解析をフル動員して、いろんな数学を組み合わせなければならない。実際、Manin予想はとても学際色の高い問題で、いろんな分野の数学者がこの予想に取り組んでいます。それだけこの予想を重要だと考える数学者が多いということであり、そのような問題に取り組むことは多くの新しい数学を生み出す可能性を秘めているのです。

難解な研究内容を丁寧に熱く説明してくださる谷本氏

──数学の研究には、このようなケースが多いのでしょうか。

谷本　必ずしもそうではありませんが、ディオファントス幾何学の問題は基本的に、それを解こうとする中で新しい数学が生まれるところに価値があるものが多い、と言えるかもしれません。

そして、そうやって思わぬ形で生まれた新しい数学は、実は社会の中でも大きく生かされています。例えば、現代の暗号技術には、代数幾何や数論が使われていますが、そのように使われるとはその分野の研究者たちも想像していないことでした。数学は、何がどんな形で役に立つかわかりません。そこに数学を研究する一つの大きな意味があると言えます。

Manin予想を“危機”から救い出した研究

──ディオファントス幾何学、そしてManin予想について研究する背景がよくわかりました。では、谷本先生ご自身がManin予想のどのような点について研究されているのか、教えてください。

谷本　私はこれまで、Manin予想についてさまざまな側面から研究してきましたが、中でも重要と言える研究を挙げると、「例外集合」についての研究があります。

Manin予想は、Fano多様体上の有理点の個数には一定の法則があり、それがある一つの式によって表現できるという予想ですが、その有理点の一部は、Fano多様体上の直線部分など、多様体の全体から言えば例外的なところに集積していることがあります。そうした例外的な有理点、すなわち例外集合は、多様体の本質を見えなくさせることがあります。そのため、それらは取り除いて考えなければならないのですが、この点に関連して、90年代にはManin予想に対する反例も登場し、実はManin予想は成り立たないのではないかとも言われるようになりました。そうした中で私は、共同研究者とともに、例外集合を幾何的に定義して、それをどう扱うべきかを明確にする証明を行いました（※2）。そしてこの証明によって、反例とされたものの持つ意味がはっきりわかり、やはりManin予想は成り立つということへの信ぴょう性が上がりました。そうしたことから、業界内ではかなり注目される研究成果となりました。

──それはすごいですね。Manin予想を危機から救い出すような研究だったんですね。では、現在特に注力しているのはどのような研究でしょうか。

谷本　最近は、Manin予想の曲線版といえる「幾何的Manin予想」を提唱していて、それについて集中的に研究を進めています。Manin予想が多様体上の有理点を数えるのに対して、こちらでは、多様体上の曲線を数える。ここには数学上の重要なアナロジーがあり、幾何的Manin予想について理解していくことは、代数多様体の性質を解き明かすことにつながっていくと考えています。

自分が生きているうちにおそらく証明はされないが…

──Manin予想の証明は、現在どのような段階にあるのですか。近い将来証明されそう、といった状況だったりするのでしょうか。

谷本　Manin予想の研究が始められてからすでに30年が過ぎていますが、証明される目処は実は全く立っていません。Manin予想は、あらゆる次元のあらゆるFano多様体についての予想なのですが、冒頭に紹介した\(x^3+y^3+z^3+w^3=0\)
という方程式のような、3次曲面の場合についてもまだ証明できていないのです。これについて証明されるだけでも、業界内では大変なニュースになると思います。それくらい、証明はできていません。私が生きているうちに証明されることはおそらくないだろうと思っています（笑）。

──なんと、そうなんですね。証明することができないならもう…、とモチベーションが下がったりすることはないのですか。

谷本　予想というのはある意味、解けちゃったらそれで終わりなんです。証明できたら、人々が職を失うという事態になる（笑）。もちろん証明できれば最高ですけど、証明はされずとも、Manin予想の研究を通じてすでに新たな数学がたくさん生み出されています。そういう意味で、証明できずとも研究する価値はすごくある。それにやはり数学者はみな、ただ面白いからやっているという側面も大きいので、証明できるかできないかは必ずしも一番重要ではないと言えるかもしれません。

いまは数学に専心する谷本氏だが、中学時代からエレキギターを弾き、高校時代にはハードロックのバンドも

人と議論することが数学研究の楽しさ

──谷本先生がManin予想の研究をされるようになった経緯を教えてください。

谷本　私は高校生の頃は、理論物理に憧れていて、超弦理論などについて勉強してみたいと考えていました。夏休みに物理の先生が特殊相対性理論の講義をしてくれて非常に興奮したことを覚えています。

しかし東京工業大学に入って数学や物理を学んでいるうちに、自分は物理の数学的な定式化に興味があるということに気づき、 2年次には数学科に進学することを選びました。そして4年次の研究室所属のとき、理論物理とも深いつながりがある代数幾何学の研究室に入り、その後大学院は、アメリカに住んでみたいという思いもあってニューヨーク大学に進学しました。

ニューヨーク大学大学院修了時に

そしてその2年次で指導してもらうことになったのが、Manin予想の専門家であるユーリ・チンケル（Yuri Tschinkel）先生でした。 2年次進級時に資格試験を突破して、さあ研究だというところで、先生にManin予想の問題を出されました。この問題を明日までに解いてきなさいと（笑）。それがきっかけで、Manin予想について研究することになりました。

──数学の研究はどのように進められるものなのでしょうか。谷本先生の研究のスタイルについて教えてください。

谷本　自分の場合、大きな問題に取り組む際は、まずはどう解いたらいいかという戦略を立て、問題を小さなステップにわけていきます。そのステップを一つずつ解決していくことを目指すのですが、その際に私はとにかく、いろんなアイデアを試して、計算して、そのまま論文のような形で証明を書いていきます。すると、ここがだめだとかうまくいかないとかが見えてくる。そこでまた別なアイデアを試してみる……ということを繰り返します。

また、私は人と議論することを大切にしています。他の数学者にアイデアを話して意見を聞く。相手のアイデアを聞いて意見を伝える。そうした中で、新しいアイデアが生まれて、道が開けたりするんです。先のManin予想の例外集合に関する証明は、ボストン・カレッジのブライアン・レーマン（Brian Lehmann）との共同研究ですが、彼とはとても親しくてよく一緒に議論し、論文を書いています。専門分野で言うと、彼が代数幾何寄りで私が数論幾何寄り。二人の知識がうまく合わさることで、いろんな研究結果を出すことができています。二人だけの知識では足りないというときは、別の研究者にも声をかけて、その人にも協力してもらう、ということをよくやっています。

──数学者は、どちらかというと一人で研究する人が多いのかなと思っていました。

谷本　日本では確かに、一人で研究を進める人が多い印象があります。私は、大学院やポスドクの時代をアメリカやデンマークで過ごしたこともあって、共同研究者がほとんど海外の人なのですが、特にアメリカの数学者は、他の人と議論しながら研究を進める人がほとんどだと思います。私にとってはそれが数学を研究する楽しさでもあるんですよね。

その意味でコロナ禍の間は、ブライアンらと直接会って議論することができなかったのが辛かったです。当時もZoom上では毎週のように話していましたが、最近また海外に行くことができるようになって、頻繁に対面で議論するようになると、Zoom上では数カ月かかってたようなことが1週間で済んだりして、会うことの大事さを改めて感じさせられています。

レーマン博士とはZoomでも頻繁に議論

数学がなければ、いまの社会はない

──最後にあえて伺いますが、数学の研究は一般に、すぐ何かの役に立つというものではないような印象があります。ただそれでも、数学の研究はきっとこれからも重要であり続けるとも感じます。数学を研究する意味は何か。先生の思いを改めて聞かせてください。

谷本　数学を研究して何になるのか、と思う人は少なくないかもしれません。しかし、情報科学、AI、暗号技術など、現代の社会において重要な役割を果たしている技術の裏には、数学の新しい知見がとても多く生かされています。数学の研究がなければ、いまの社会はありえません。

でも一方で、この分野を研究したらこう役に立つ、とは言えないのも数学の特徴です。つまり、数学が起こすイノベーションというのは、予測不可能なんです。目的もなくただ「面白いから」という気持ちで研究に取り組んでいったら、その結果が思わぬ形で社会を変えたりするのが数学なのです。私は数学のそういうところに、価値や面白さを見出して研究をしています。これからもそんなことを意識しながら、どんどん新しいことにチャレンジしていきたいです。

また、高校で数学を学ぶと「数学ってまだ何か研究することあるの？」って気持ちになるかもしれませんが、数学には本当にまだまだやることがいっぱいあります。数学の道に進もうかなと思っている人は、ぜひ思い切って、数学科の門を叩いてみてほしいです。

──ありがとうございました！

（※1）代数多様体の分類のうち、主要なものの一つ。2次曲線や3次曲面なども含まれ、比較的扱いやすいタイプと言える。
（※2）Brian Lehmann, Sho Tanimoto. “On the geometry of thin exceptional sets in Manin’s conjecture.” Duke Mathematical Journal, 166(15) 2815-2869 15 October 2017.
https://doi.org/10.1215/00127094-2017-0011

この一冊	『The Martian』（Andy Weir著 、Penguin Random House 社）本書は、マット・デイモン主演で『オデッセイ』というタイトルで映画化され、日本語版の題名は『火星の人』。谷本氏は、英語版で読んだとのこと。「火星に取り残された宇宙飛行士が、地球に戻るためにサバイバルする様子を書いた小説で、面白くて大変気に入りました。著者のアンディ・ウィアーはサイエンスにすごく詳しくて、この本は物理や工学という面でもとても面白い。彼の小説は大体読むようにしています」
いつもそばにあるもの	谷本氏がまず挙げたのは、愛用のMacBookでした。 論文を書くのになくてはならないアイテムとのこと。「意外だと思われるかもしれませんが、 僕はあまり紙とペンは使いません。 家にホワイトボードがあるので、計算はその上で行って、その結果を直接Macbookに打ち込んで論文に書き起こします。あと、アイテムではないですが、 高校の頃から支えてくれる妻、そして息子と娘（10歳と3歳 *取材日時点）の支えはいつもありがたく、やはり何よりも大切です！」

谷本 祥 （たにもと・しょう）

名古屋大学大学院多元数理科学研究科 准教授。東京工業大学卒業後、ニューヨーク大学でMaster of Science（数学）、Ph.D.（数学）を取得。その後、米テキサスのライス大学、デンマークのコペンハーゲン大学を経て、2018年から熊本大学大学院先導機構准教授。2021年より現職。専門分野は、代数幾何・数論幾何。本文中でも触れた、Manin予想の例外集合に関する共著論文“On the geometry of thin exceptional sets in Manin’s Conjecture”は、2017年に、影響力の大きい学術誌 Duke Mathematical Journal に掲載された。