ソフト粒子の研究は、まだまだ新しい切り口が沢山あると考えています。物理や数値シミュレーションを使って、日々異なる見方や考え方をするのが楽しみです。
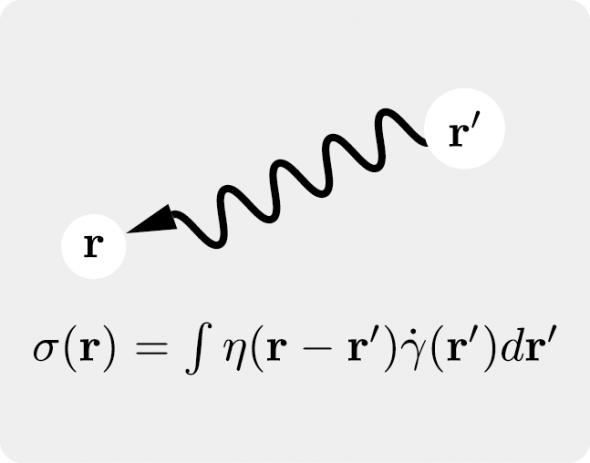
本研究の最初の成果は粒子間に接線力が働く場合の線形応答に関するものである。ここでは、擬二次元的に配置した球形粒子を考え、粒子間に接線方向の弾性力を導入する。粒子が平衡位置の周りで微小振動する場合を調べるため、クーロン摩擦など塑性的な変形は考慮しない。これにより、各粒子の回転自由度を加えたダイナミカル・マトリックスを計算することができ、微小なせん断変形に対する粒子系の剛性率の表式が得られる。但し、剛性率の表式はダイナミカル・マトリックスの固有値と固有ベクトルを含んでおり、ダイナミカル・マトリックスの各要素は粒子の平衡位置を与えて初めて決定される。従って、分子動力学法で求めた粒子位置を使ってダイナミカル・マトリックスの各要素を決定し、数値的に固有値と固有ベクトルを求めることで剛性率を計算した。計算した剛性率は分子動力学法で直接求めた剛性率とほぼ100%一致し、数値データのインプットが必要ではあるものの、粒子系の剛性率を理論的に予測することに成功した。また、定常せん断下における粒子系の応力についても同様の解析を行い、急激な応力降下(アバランチ)が起こる場合を除き、分子動力学法による数値計算の結果をほぼ100%説明することができた。
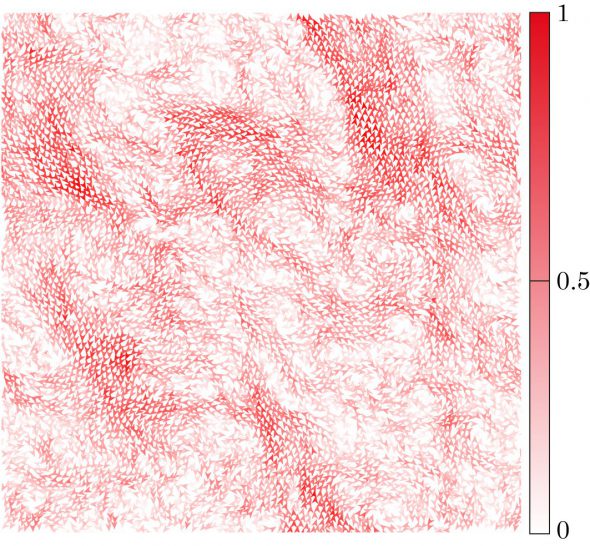
本研究の次の成果は粒子系の応力降下(アバランチ)に関するものである。アバランチ現象はナノスケールの物体からマクロなスケールの物体まで普遍的に観測され、応力降下の大きさは同一の指数を持った冪分布に従うとされている。地震もアバランチ現象の一種で、これまで多くの理論的・数値的研究が行われてきたものの、実測されるアバランチの統計則と数値計算の結果には一定の隔たりがあった。そこで、分子動力学法によって粒子系のせん断変形をシミュレートし、接触する粒子間に働く摩擦力の効果に注目して研究を行った。その結果、摩擦のない数値計算では見過ごされていた小さなアバランチが重要な役割を果たし、応力降下の大きさの分布や様々な統計則が実測や理論的な予測に近づくことを明らかにした。この研究成果は学術誌The European Physical Journal Eの論文として掲載されると同時に、学術誌の表紙にも取り上げられた(図)。

http://dx.doi.org/10.1140/epje/s10189-021-00089-8
理工系領域