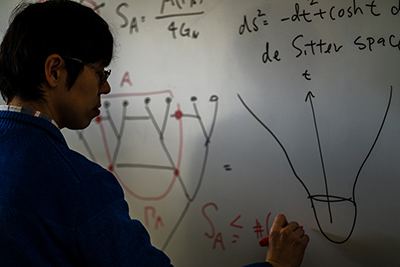InaRIS フェロー (2020-2029)

高柳匡 Tadashi Takayanagi

京都大学基礎物理学研究所教授※助成決定当時

2020InaRIS理工系

website researchmap

採択テーマ: 量子エンタングルメントから創発する量子重力理論

キーワード

研究概要: 重力のミクロな物理法則である「量子重力理論」を解明する糸口として、高柳氏が発見した「笠ー高柳公式」が注目されている。この公式は「エンタングルメント・エントロピー」とよばれるミクロな情報量が宇宙の面積と等しいという関係式であり、重力理論の宇宙は量子情報から創発することを示唆している。本研究では、独創的なアイデアをさらに発展させて量子重力理論を解明することを目的とし、私たちの宇宙がどのように生まれたのか、そのミクロな起源に迫る。

助成を受けて

InaRIS に応募した理由は、10 年という長い期間にわたって支援していただけるからです。私の研究は基礎研究で、腰を据えてじっくり取り組む必要があり、長期間サポートいただけるのは大変ありがたいです。InaRIS の支援を受けて、我々の宇宙がどうやって誕生したのか、根源的な問題に挑戦したいです。

フェロー紹介動画

情報公開

成果報告（3年目）選考理由

従来のゲージ重力対応は宇宙定数が負の宇宙を対象としていたが、当フェローは、現実の宇宙のように正の宇宙定数を持つ「ドジッター宇宙におけるゲージ重力対応」を3次元時空の場合に見出した。また、「擬エントロピー」という新しい量子情報量を導入することにより、ゲージ重力対応において虚時間に依存する重力理論の空間を量子情報の視点で記述することに成功した。さらに、楔型の宇宙に置かれた重力理論が、その先端に局在する場の量子論に対応するという「ウェッジ・ホログラフィー」を発見した。関連手法を用いて、ブラックホールの蒸発を記述する模型を考案し、蒸発がユニタリーな過程であることを意味するページ曲線を導出した。

これまでの研究成果として、特に、①3次元ドジッター宇宙のゲージ重力対応、②ゲージ重力対応と擬エントロピー、③ウェッジ・ホログラフィー、④動く鏡の模型とページ曲線、の４つのハイライトを選んで以下では詳しく述べる。

① 3次元ドジッター宇宙のゲージ重力対応
ゲージ重力対応はAdS/CFT対応とも呼ばれ、d+1次元の反ドジッター宇宙(AdS宇宙)とd次元の共形場理論（場の量子論がスケール対称性を持つ特殊な場合の理論、CFTと呼ぶ）が等価になるという対応関係である。これによって、理論物理学の難問である量子重力理論の問題を、重力を含まない量子多体系の理論に結びつけて理解することが可能となる。しかし、反ドジッター宇宙は宇宙定数（ダークエネルギー）が負の値をとり、一方で現実の宇宙は観測などから、正の値をとるドジッター宇宙と考えられている。従って、ゲージ重力対応のドジッター宇宙への一般化(dS/CFT対応と呼ばれる)は極めて重要な課題であるが、対応する共形場理論が分からないので、これまでほとんど進展が見られなかった。しかし、本研究では、3次元の重力理論とChern-Simonsゲージ理論の対応関係と、Chern-Simons理論と2次元WZW模型と呼ばれる共形場理論の関係、を利用することで、具体的にd=2つまり3次元のドジッター宇宙に等価になる共形場理論を発見した。
これはSU(2)WZW模型のレベルと呼ばれるパラメーターを複素数にとって得られる共形場理論で与えられ、共形場理論による計算と重力理論から予想される3次元ドジッター宇宙の分配関数が一致することを確かめた。この成果は、Physical Review Letter誌に出版され、Editor’s Suggestionに選ばれた。さらに、米国物理学会のアウトリーチ雑誌であるPhysics誌のViewpoint記事に取り上げられた。

② ゲージ重力対応と擬エントロピー
当フェローらが2006年に発見したゲージ重力対応において、共形場理論のエンタングルメント・エントロピーが、対応する重力理論の宇宙における極小曲面の面積と等しい、
という公式は、量子情報から宇宙が創発することを示唆し、このような考え方が超弦理論の最近の潮流となっている。当フェローは、量子情報理論の研究者である中田芳史らと共同で、虚時間の時間発展を取り入れた、より一般の重力理論の宇宙を考えると、エンタングルメント・エントロピーではなく、それを一般化した「擬エントロピー」が極小曲面の面積に一致することを見出した。またあるクラスの量子状態に対しては、擬エントロピーは、始状態と終状態の中間状態から抽出できるエンタングルメント・エントロピーの量と等しいという操作的な解釈も与えた。その後の研究で、擬エントロピーが量子イジング模型の量子相を分類する際に秩序変数として機能することを見出し、その成果はPhysical Review Letter誌に出版された。

③ ウェッジ・ホログラフィー
ゲージ重力対応は、反ドジッター宇宙における重力理論が、それよりも1次元低い時空の共形場理論と等価になる対応であるが、当フェローは、反ドジッター宇宙のおける楔型（ウェッジ型）の領域に着目すると、その領域における重力理論は、楔の先端に相当する２次元低い時空における共形場理論と等価になることを見出した。分配関数・相関関数・エンタングルメント・エントロピーが、この対応で両者が一致することを示した。この成果は、Physical Review D誌に掲載され、Editor’s suggestionに選ばれた。

④ 動く鏡の模型とページ曲線
動く鏡の模型は、時間に依存する境界を持つ場の量子論の模型で、鏡の軌跡をうまく選ぶとブラックホールからのホーキング輻射を記述できることが知られている。ブラックホールがホーキング輻射で蒸発する際に、蒸発後に一見、混合状態になり、時間発展において、量子論の基礎であるユニタリー性が破れるように見える、これがブラックホールの情報損失問題である。この問題を回避するには、輻射のエンタングルメント・エントロピーがページ曲線に従う必要がある。当フェローは２次元の動く鏡の模型を共形場理論の手法で解析し、エンタングルメント・エントロピーの時間変化を解析的に計算できることを示した。ブラックホールの蒸発を模した動く鏡の模型に対して、エンタングルメント・エントロピーを計算し、その時間発展が理想的なページ曲線に従うことを導いた。この模型は、一見、重力入っていない場の量子論であるが、ゲージ重力対応を部分的に用いると実は、蒸発するブラックホールと共形場理論が相互作用する系とみなすことができる。従って、上記の成果によって、ブラックホールの蒸発でユニタリティーが破れない証拠が得られたと言える。この成果はPhysical Review Letter誌に出版された。

基礎物理学におけるもっとも重要な問題の一つは、重力のミクロな物理法則を完全に理解すること、すなわち量子重力理論を解明することである。高柳匡氏が笠真生氏と2006年に発表したエンタングルメント・エントロピーのホログラフィックな導出（笠ー高柳公式）は、J. Maldacena氏が1997年にAdS/CFT対応（反ドシッター空間ー共形場理論対応）を提案して以来の最も重要かつ画期的な発見のひとつであり、この分野の流れを大きく変える影響力があった。たとえば、E. Witten氏は、2014年に京都賞を受賞した際のインタビューにおいて、「21世紀になってからのハイライト」として真っ先に笠ー高柳公式を挙げている。笠ー高柳公式はAdS/CFT対応に基づく微視的な説明がなされたことで、理論物理学における重要な公式として確立している。

高柳氏は以来14年間にわたって笠ー高柳公式を発展させ、ホログラフィー原理の仕組みの解明とその応用に主導的な貢献をしてきた。たとえば、高柳氏とM. Headrick氏は、フォン・ノイマン・エントロピーの強劣加法性と呼ばれる不等式が、笠ー高柳公式においては極小曲面の三角不等式という幾何学的な性質に帰着することを見出している。エントロピーの持つ深い性質が重力理論の幾何学的構造に反映されているというこの発見は、この分野のその後の発展を大いに刺激した。また、ここ数年にわたり、ホログラフィー原理の微視的なメカニズムにおいて、量子情報理論における量子誤り訂正符号が重要な役割を果たしていることが明らかになってきた。このメカニズムの解明においても、笠ー高柳公式は本質的な役割を果たしている。

高柳氏の提案研究では、このように「笠ー高柳公式」を契機として広がってきた「量子情報」と「重力理論の宇宙」との深い関係性に関する新しい考え方をさらに推し進め、未だ発展途上にある量子重力理論の解明へ向けたブレークスルーを目指している。関係する高柳氏の最近の研究としては、「純粋化エンタングルメント」と呼ばれる混合状態に対してエンタングルメント・エントロピーを拡張した量が、AdS/CFT対応である種のワームホールの断面積に一致することを見出し、また、共形場理論の経路積分を離散化して計算する場合に、最も効率良く離散化することを要請すると自然に反ドジッター空間の幾何が現れることを発見したことなどが挙げられ、その新しい発展が注目されている。

ホログラフィー原理におけるエンタングルメント・エントロピーの公式の発見と、その後の発展における高柳氏の一連の研究は、量子重力理論や超弦理論の基礎的な成果であり、また同氏の研究は物性理論や量子情報理論との連携も促進している。このような研究成果に加えて、高柳氏は指導者としても優れており、彼の薫陶を受けて、すでに多くの若手研究者が育っている。高柳氏は、超弦理論研究の世界的なリーダーであり、InaRISフェローシップの支援により今後10年の日本における理論物理学研究を牽引することが期待される。